Sur certaines surfaces algébriques

Proposons-nous d’étudier, au point de vue de l’Analysis situs, la surface

$$\tag{1} z=\sqrt{F(x,y)},$$

où $F(x,y)$ est un polynome [1]. Nous supposerons que la courbe

$$F(x,y)=0$$

ne présente que des points ordinaires où $\frac{dF}{dx}$ n’est pas nul, ou bien $\frac{dF}{dx}=0$, mais sans que $\frac{d^2F}{dx^2}$ ni $\frac{dF}{dy}$ s’annulent, ou des points doubles ordinaires où

$$\frac{dF}{dx}=\frac{dF}{dy}=0,$$

mais sans que $\frac{d^2F}{dx^2}$ ni $\frac{d^2F}{dx^2}\frac{d^2F}{dy^2}-\left(\frac{d^2F}{dxdy}\right)^2$ s’annulent.

Considérons d’abord $y$ comme une constante. Alors l’équation (1) représentera une courbe algébrique et les coordonnées $x$ et $z$ d’un point de cette courbe pourront s’exprimer, comme on le sait, comme des fonctions fuchsiennes d’une même variable auxiliaire $u$. Considérons le groupe fuchsien correspondant et le polygone fuchsien qui l’engendre. En général, le polygone fuchsien qui correspond à une courbe de genre $p$ est un polygone de $4p$ côtés, et l’on peut supposer, soit que les côtés de rang $4q+1$ et $4q+3$ comme les côtés de rang $4q+2$ et $4q+4$ sont conjugués (ce qui correspond aux périodes dites normales des fonctions abéliennes), soit que les côtés opposés sont conjugués.

C’est cette dernière hypothèse que nous adopterons.

Je rappelle d’ailleurs que la somme des angles du polygone doit être égale à $2\pi$. Mais, dans le cas particulier de la courbe (1), on est dans le cas dit hyperelliptique, c’est-à-dire que les fonctions abéliennes correspondantes se réduisent à des fonctions hyperelliptiques.

Dans ce cas, on sait que notre polygone fuchsien admet un centre de symétrie et se décompose en deux polygones de $2p+1$ côtés symétriques l’un de l’autre par rapport à ce centre.

Avant d’aller plus loin, je précise ce que j’entends par ce mot symétrie. Nous nous plaçons en ce moment au point de vue de la géométrie non-euclidienne ; je veux dire que nous considérons comme des droites non-euclidiennes les cercles qui coupent orthogonalement le cercle fondamental ; nous disons que deux figures sont symétriques par rapport à une droite non-euclidienne quand on peut passer de l’une à l’autre par une inversion (transformation par rayons vecteurs réciproques) qui n’altère pas cette droite non-euclidienne ; nous disons que deux figures sont égales quant elles sont symétriques d’une même troisième par rapport à deux droites non-euclidiennes rectangulaires passant par ce centre.

Cela posé, notre polygone $R$ de $4p$ côtés se décompose en deux polygones $R'$ et $R''$ de $2p+1$ côtés symétriques l’un de l’autre par rapport à un centre.

Nous pouvons supposer que le polynome $F(x,y)$ n’est divisible par aucun carré. Dans ces conditions, l’équation en $x$

$$F(x,y)=0$$

n’aura pas de racine double, sauf pour certaines valeurs singulières de $y$. Elle aura $2p+2$ racines simples que j’appelerai

$$x_0,x_1,x_2,\ldots,x_{2p+1},$$

Alors $x_0$ correspondra aux $2p+1$ sommets du polygone $R'$, tandis que $x_1,x_2,\ldots,x_{2p+1}$ correspondront aux milieux (toujours au point de vue non-euclidien) des $2p+1$ côtés.

Dans le plan des $x$, nous pourrons tracer $2p+1$ coupures

$$C_1,C_2,\ldots,C_{2p+1}$$

allant du point $x_0$ aux points $x_1,x_2,\ldots,x_{2p+1}$, et de telle façon qu’aux deux lèvres de la coupure $C_i$ correspondront sur le polygone $R'$ les deux moitiés du $i^{\textrm{ième}}$ côté.

Dans le cas de $p=1$ (c’est-à-dire si l’équation $F=0$ est du quatrième degré en $x$), le polygone $R$ se réduit à un parallélogramme, les polygones $R'$ et $R''$ à deux triangles rectilignes et les fonctions fuchsiennes à des fonctions elliptiques.

Qu’arrivera-t-il maintenant si, faisant varier $y$ d’une manière continue, cette variable revient à sa valeur initiale ?

Notre groupe fuchsien variera d’une manière continue, de même que $x_0,x_1,\ldots,x_{2p+1}$ et que le polygone fuchsien $R$. Quand $y$ aura fait un tour complet, le groupe fuchsien sera redevenu le même ; les points $x_i$ se seront en général permutés entre eux et le polygone $R$ sera devenu un autre polygone $R_1$, équivalent à $P$, je veux dire susceptible d’engendrer le même groupe fuchsien.

Prenons, par exemple, le cas de $p=1$ ; le polygone $R$ est un parallélogramme dont les côtés $\omega$ et $\omega'$ représenteront en grandeur et en direction les deux périodes d’une fonction elliptique. Quand $y$ aura décrit un tour complet, notre parallélogramme sera devenu $R_1$ dont les côtés représenteront encore en grandeur et en direction deux périodes de la même fonction elliptique ; seulement ces périodes ne seront plus, en général, $\omega$ et $\omega'$ mais deux périodes équivalentes

$$\alpha\omega+\beta\omega',\ \ \gamma\omega+\delta\omega',$$

où $\alpha,\beta,\gamma,\delta$ sont quatre entiers tels que $\alpha\delta-\beta\gamma=1$.

Ceci nous ramène à un premier rapprochement avec l’Analysis situs. Supposons que $p=1$ ; supposons que l’on convienne de donner à $y$ une quelconque des valeurs situées sur un certain contour fermé $K$, à $x$ une valeur complexe quelconque, et que $z$ soit défini par l’équation (1). L’ensemble de ces points $x,y,z$ constituera une certaine variété fermée $V$ à 3 dimensions. Quelles sont les propriétés de cette variété du point de vue de l’Analysis situs ?

A chaque point de cette variété je ferai correspondre trois variables réelles $\xi,\eta,\zeta$ définies comme il suit : $\zeta$ sera fonction de $y$ seulement et augmentera de $1$ quand $y$ aura décrit son tour complet. Quant à $\xi$ et $\eta$, ce seront des fonctions linéaires des parties réelle et imaginaire de l’intégrale elliptique $u$ définie par l’équation (1). Ces fonctions linéaires seront telles que $\xi$ et $\eta$ se changent en $\xi+1,\eta$ quand cette intégrale elliptique augmente de $\omega$ et en $\xi,\eta+1$ quand elle augmente de $\omega'$ (de telle façon que $u=\xi\omega+\eta\omega'$). Dans ces conditions, on retombera sur un même point de la variété $V$ quand $\xi,\eta,\zeta$ se changeront en

$$\xi+1,\eta,\zeta$$

ou en

$$\xi, \eta+1,\zeta$$

ou en

$$\delta\xi-\gamma\eta, \beta\xi+\alpha\eta, \zeta+1,$$

car si $\xi_1$ et $\eta_1$ sont ce que deviennent $\xi$ et $\eta$ quand on change $\zeta$ en $\zeta+1$, on aura

$$u=\xi\omega+\eta\omega'$$

et, d’autre part,

$$u=\xi_1(\alpha\omega+\beta\omega')+\eta_1(\gamma\omega+\delta\omega'),$$

ou plus généralement quand $\xi,\eta,\zeta$ subiront une transformation quelconque du groupe $G$ engendré par ces trois transformations.

On reconnaît là le groupe considéré dans l’Analysis situs, page $237$, $6^e$ exemple. La variété $V$ est donc homéomorphe à la variété envisagée dans ce $6^e$ exemple et elle admet $G$ comme groupe fondamental (cf Analysis situs, paragraphe 12).

Définissons toujours la variété de la même manière mais ne supposons plus $p=1$. Alors $R$ est un polygone fuchsien curviligne. Nous introduirons encore trois variables $\xi,\eta,\zeta$ ; cette dernière $\zeta$ sera définie comme plus haut. Quant à $\xi$ et $\eta$, ce seront des fonctions bi-uniformes de $\zeta$ et des parties réelle et imaginaire de la variable $u$ ; de telle façon qu’à toute valeur complexe de $u$ corresponde un système de valeurs de $\xi$ et de $\eta$, et un seul, et inversement. A chaque valeur de $\zeta$ correspondra un groupe fuchsien et le polygone fuchsien $R$ relatif à ce groupe. Ce groupe fuchsien sera engendré par $2p$ substitutions

$$S_1,S_2,\ldots, S_{2p}.$$

La substitution $S_k$ changera $\xi$ et $\eta$ en

$$\phi_k(\xi,\eta,\zeta),\ \ \psi_k(\xi,\eta,\zeta),$$

de sorte que nous retomberons sur un même point de la variété $V$ quand nous changerons $\xi,\eta,\zeta$ en

$$\phi_k(\xi,\eta,\zeta),\ \ \psi_k(\xi,\eta,\zeta),\ \ \zeta.$$

Nous pouvons d’ailleurs définir les fonctions $\xi,\eta$ de telle façon que $\phi_k$ et $\psi_k$ ne dépendent pas de $\zeta$.

En effet, envisageons la figure formée par le polygone fuchsien $R=R'+R''$ et par ses transformés par les diverses substitutions du groupe fuchsien. Ce polygone et ses transformés remplissent la surface du cercle fondamental. La figure ainsi formée se déformera d’une manière continue quand on fera varier $\zeta$ de manière continue, mais elle restera homéomorphe à elle-même. On pourra donc faire correspondre à tout point $M_0$ de cette figure dans sa position initiale un point $M$, et un seul, de la même figure dans une quelconque de ses positions consécutives, et cela de telle sorte que :

1. Que le point $M$ se déplace d’une manière continue quand $\zeta$ varie d’une manière continue ;
2. Que, si $M_0$ est un sommet de $R$, $M$ reste un sommet de $R$ ; que, si $M_0$ est sur un côté de $R$, $M$ reste sur un côté de $R$ ;
3. Que, si deux points $M_0$ et $M_0'$ sont congruents (c’est-à-dire transformés l’un de l’autre par une des substitutions du groupe fuchsien), les points $M$ et $M'$ soient également congruents.

Je supposerai alors que les valeurs des deux variables auxiliaires $\xi$ et $\eta$ sont les mêmes pour le point $M_0$ et pour le point $M$ ; je supposerai, par exemple, que ce sont les coordonnées du point $M_0$.

Dans ces conditions, $\phi_k$ et $\psi_k$ ne dépendent pas de $\zeta$.

Quand, $y$ ayant fait un tour complet, $\zeta$ aura augmenté de $1$, le polygone $R$, en se déformant successivement, sera devenu un polygone $R_1$, équivalent à $R$.

Le point $M$ sera venu en un point $M_1$ dont les coordonnées seront

$$\theta(\xi,\eta), \ \ \theta_1(\xi,\eta).$$

On voit que l’on retombe sur un même point de $V$ quand $\xi,\eta,\zeta$ se changent en

$$\theta(\xi,\eta),\ \ \theta_1(\xi,\eta),\ \ \zeta+1,$$

ou, plus généralement, quand $\xi,\eta,\zeta$ subissent une des substitutions du groupe $G$ engendré par les $2p+1$ substitutions qui changent $\zeta$ et $\eta$ en

$$\phi_k,\ \ \psi_k,\ \ \zeta\ \ (k=1,2,\ldots,2p)$$

ou en

$$\theta,\ \ \theta_1,\ \ \zeta+1.$$

Ce groupe $G$ sera donc le groupe fondamental de la variété $V$.

Nous remarquerons d’abord que ce groupe n’est pas simple. Nous pouvons appeler $G'$ le groupe engendré par les $2p$ substitutions $(\phi_k,\psi_k,\zeta)$ et $\Sigma$ la substitution $(\theta,\theta_1,\zeta+1)$. Je dis que $G'$ est un sous-groupe invariant de $G$ ; il suffit de montrer que $G'$ est permutable à $\Sigma$. En effet, $\Sigma$ changeant le polygone $R$ en un polygone équivalent, n’altère pas le groupe fuchsien. Or, le groupe fuchsien n’est autre chose que le groupe engendré par les $2p$ substitutions $(\xi,\eta;\phi_k,\psi_k)$ ; on voit que ce groupe est permutable à la substitution $(\xi,\eta;\theta,\theta_1)$ et le théorème énoncé s’en déduit immédiatement.

Considérons maintenant une variété $V$ définie comme il suit :

Représentons la variable $y$ sur une sphère. Distinguons sur cette sphère les points ordinaires pour lesquels l’équation $F(x,y)$ n’a pas de racines multiples et les points singuliers pour lesquels cette équation a des racines multiples.

Soient $O$ un point ordinaire et $A_1,A_2,\ldots,A_q$ les points singuliers. Joignons $O$ à chacun de ces points par des coupures $OA_1,OA_2,\ldots,OA_q$ ne se coupant pas mutuellement.

D’autre part, traçons autour de chacun des points singuliers un cercle de rayon très petit que nous appellerons cercle de garde.

Pour former la variété $V$, nous donnerons à $y$ une valeur quelconque non comprise dans l’un des cercles de garde, à $x$ une valeur complexe quelconque, à $z$ une des deux valeurs définies par l’équation (1).

A chaque valeur de $y$ correspondra un polygone fuchsien $R$, et ce polygone est parfaitement déterminé si $y$ est assujetti à varier sans franchir les coupures $OA$ ; car c’est seulement quand $y$ fait un tour complet en tournant autour de l’un des points singuliers $A$ que le polygone $R$ peut s’échanger contre un polygone équivalent.

Le polygone $R$ et ses transformés par le groupe fuchsien forment une figure qui, quand $y$ varie d’une manière continue, se déforme aussi d’une manière continue, mais en restant toujours homéomorphe à elle-même. Soit alors $y_0$ une valeur initiale de $y$, $R_0$ le polygone $R$ correspondant, un point $M_0$ du plan de $R_0$ ; nous pouvons faire correspondre au point $M_0$ un point $M$ du plan de $R$, de telle façon que les coordonnées de $M$ soient des fonctions continues et bi-uniformes de celles de $M_0$ ; que $M$ soit en un sommet ou sur un côté de $R$, si $M_0$ est en un sommet ou sur un côté de $R_0$ ; que $M$ et $M'$ soient congruents si $M_0$ et $M_0'$ sont congruents.

Nous pourrons ensuite faire correspondre au point $M$ deux variables auxiliaires $\xi$ et $\eta$ qui ne seront autre chose que les coordonnées de $M_0$. Dans ces conditions, le groupe fuchsien sera dérivé de $2p$ substitutions

$$S_1,S_2,\ldots, S_{2p},$$

telles que $S_k$ change $\xi$ et $\eta$ en $\phi_k(\xi,\eta), \psi_k(\xi,\eta)$, les fonctions $\phi_k$ et $\psi_k$ étant indépendantes de $y$.

Quand $y$ tourne autour du point singulier $A_i$, $R$ se change en un polygone équivalent $R_1$ ; il en résulte que $\xi$ et $\eta$ se changent en

$$\theta_i(\xi,\eta),\ \ \theta_i'(\xi,\eta),$$

$\theta_i$ et $\theta_i'$ étant des fonctions bi-uniformes et continues de $\xi$ et $\eta$, telles que, quand le point $\zeta,\eta$ est en un sommet ou sur un côté de $R_0$, le point $\theta_i,\theta_i'$ est en un sommet ou sur un côté du polygone $R_1^0$ analogue à $R_i$ et équivalent à $R_0$.

Envisageons maintenant un second groupe fuchsien que j’appellerai $\Gamma$, de telle façon que $y$ soit une fonction fuchsienne de la variable auxiliaire $\zeta+i\zeta'$ admettant ce groupe $\Gamma$. Le polygone fuchsien $P$ correspondant sera de la deuxième famille (c’est-à-dire qu’il aura tous ses sommets sur le cercle fondamental et tous ses angles nuls) et de genre 0. Ses différents sommets correspondront aux valeurs $A_1,A_2,\ldots,A_q$ de la variable $y$.

Aux $q$ points singuliers $A_1,A_2,\ldots,A_q$ correspondront les $q$ substitutions

$$\Sigma_1,\Sigma_2,\ldots,\Sigma_q,$$

qui engendreront le groupe $\Gamma$ ; et la substitution $\Sigma_i$ changera $\zeta$ et $\zeta'$ en

$$\chi_i(\zeta,\zeta'), \chi_{i}'(\zeta,\zeta').$$

Il résulte de là qu’on retombera sur le même point de la variété $V$ quand les quatre variables $\xi,\eta,\zeta,\zeta'$ subiront une des substitutions du groupe $G$ engendré par les $2p+q$ substitutions qui changent ces variables en

$\phi_k(\xi,\eta),\ \psi_k(\xi,\eta),\ \zeta,\ \zeta'$	$(k=1,2,\ldots,2p)$ ;
$\theta_i(\xi,\eta),\ \theta'_i(\xi,\eta),\ \chi_i(\zeta,\zeta'),\ \chi_i'(\zeta,\zeta')$	$(i=1,2,\ldots,q)$.

Les $2p$ premières de ces substitutions engendrent un groupe $G'$ (qui ne sera autre que le groupe fuchsien appliqué à $\xi$ et à $\eta$, les deux variables $\zeta$ et $\zeta'$ [2] demeurant inaltérées). Ce groupe fuchsien étant permutable aux substitutions $\Sigma_i$, on conclurait, comme plus haut, que $G'$ est un sous-groupe invariant de $G$.

Ce groupe peut être regardé [3] comme le groupe fondamental de la variété $V$, pourvu que l’on suppose, comme nous l’avons fait, que $y$ est assujetti à ne pas pénétrer dans les cercles de garde.

En effet, soit $N$ le point de l’espace à quatre dimensions dont les coordonnées sont $\xi,\eta,\zeta,\zeta'$. A chaque point $N$ correspondra un point de $V$, mais à chaque point de $V$ correspondront une infinité de points de $N$ ; je dirais que ces points sont congruents entre eux.

D’après les définitions données dans l’Analysis situs (voir ici à chaque substitution du groupe fondamental de $V$ correspondra un countour fermé $K$ tracé sur $V$, le point initial du contour étant un certain point fixe choisi une fois pour toutes sur $V$ (c’est le point que j’appelais $M_0$ dans l’Analysis situs). Soit $N_0$ l’un des points $N$ correspondant à ce point fixe de $V$ ; à notre contour fermé $K$ correspondra dans l’espace $(\xi,\ \eta,\ \zeta,\ \zeta')$ une ligne $N_0BN_0'$ allant du point $N_0$ à un point congruent $N_0'$.

Il est clair ensuite que deux lignes $N_0BN_0'$, $N_0CN_0'$ ayant mêmes extrémités conduiront à une même substitution du groupe fondamental. Il suffit pour cela de faire voir que le contour fermé $N_0BN_0'CN_0$ limite une aire, car alors le contour fermé correspondant sur $V$ limitera aussi une aire et pourra se réduire à un point par déformation continue.

Il suffit donc de montrer que la région de l’espace à quatre dimensions où peut se mouvoir le point $N$ est simplement connexe. Quelle est cette région ? D’abord le point $\xi,\ \eta$ peut parcourir tout le cercle fondamental, qui est une aire simplement connexe. Quant au point $\zeta,\ \zeta'$, il peut parcourir le polygone $P$ et ses transformés par le groupe fuchsien $\Gamma$. Il pourrait donc parcourir aussi le cercle fondamental tout entier, s’il n’y avait lieu de tenir compte de l’existence des cercles de garde. Comme $y$ ne peut pénétrer dans ces cercles de garde, il faut retrancher du polygone $P$ de petites régions dans le voisinage de chaque sommet, de même pour ses transformés. Il faudra donc retrancher du cercle fondamental une infinité de petits cercles, tous extérieurs les uns aux autres et tous tangents au cercle fondamental. L’aire restante n’en étant pas moins simplement connexe, la région où peut se mouvoir le point $(\xi,\ \eta,\ \zeta,\ \zeta')$ c’est-à-dire le point $N$, est bien simplement connexe. C. Q. F. D.

Ainsi, à un point $N_0'$ (ou, si l’on veut, à la substitution du groupe $G$ qui change $N_0$ en $N_0'$) correspond une substitution du groupe fondamental, et une seule. Il résulte de là que le groupe fondamental est isomorphe à $G$ ; mais nous ne savons pas encore si l’isomorphisme n’est pas mériédrique.

C’est ce qui arriverait s’il y avait des points $N_0'$ (autres que $N_0$) tels que la substitution correspondante du groupe fondamental se réduise à la substitution identique, c’est-à-dire tels que le contour fermé tracé sur $V$ et correspondant à la ligne $N_0BN_0'$ limite une aire et puisse se réduire à un point par déformation continue.

Nous devons donc rechercher si, quand on décrit sur $V$ un contour fermé infiniment petit, il peut arriver que le point $N$ subisse une substitution de $G$ ne se réduisant pas à la substitution identique. Quand on décrira sur $V$ un contour infiniment petit, la variable $y$ décrira aussi dans son plan un contour infiniment petit. Ce contour ne pourra entourer l’un des points singuliers $A_i$, puisque chacun de ces points singuliers est protégé par un cercle de garde, très petit, mais fini, où $y$ ne peut pénétrer. Nous pourrons alors, en faisant subir à notre contour fermé une déformation infiniment petite, nous arranger pour que, $y$ restant constant tout le long du contour, la variable $x$ décrive dans son plan un contour fermé infiniment petit. Si ce contour n’entoure aucun des points singuliers $x_k$, le point $N$ dont les coordonnées sont $\xi,\ \eta,\ \zeta,\ \zeta'$ revient à sa valeur primitive, et il n’a pas subi une substitution de $G$ autre que la substitution identique. Si le contour entoure un point singulier, et un seul, la variable $z$ change de signe et le cycle n’est pas fermé sur $V$. Enfin, il ne peut arriver que le contour entoure deux points singuliers, puisqu’il est infiniment petit, que deux points singuliers ne peuvent être infiniment voisins que quand $y$ est près d’un des points $A_i$, et que nous ne pouvons approcher de ces points $A_i$ à cause des cercles de garde.

En résumé, quand on décrira sur $V$ un cycle fermé, la substitution subie par $N$ se réduira toujours à la substitution identique. Donc l’isomorphisme de $G$ et du groupe fondamental est holoédrique. En d’autres termes, puisque le groupe fondamental n’est défini que par sa forme, le groupe n’est autre chose que $G$.

On voit quel rôle jouent les cercles de garde dans le raisonnement qui précéde. [4] Supprimons maintenant ces cercles de garde et supposons que $x$ et $y$ puissent prendre des valeurs complexes quelconques, et que $V$ soit, par conséquent, la variété définie par l’équation (1).

D’abord, le groupe fondamental sera toujours isomorphe à $G$ ; je n’ai rien à changer à cette partie du raisonnement. Mais il reste à savoir si cet isomorphisme n’est pas mériédrique, et, pour le raconnaître, je vais, comme plus haut, examiner ce qui se passe quand on décrit sur $V$ un cycle fermé infiniment petit.

Si, quand on décrit ce cycle, $y$ ne tourne pas autour d’un point singulier $A_i$ ou ne reste pas infiniment voisin de $A_i$, les raisonnements précédents s’appliqueront encore et la substitution subie par $N$ se réduira à la substitution identique. Supposons maintenant que $y$ décrive un cercle fermé très petit autour de $A_i$. Alors $\zeta$ et $\zeta'$ se changeront en $\chi_i$ et $\chi_i'$ et $N$ subira soit la substitution $(\theta_i,\ \theta_i',\ \chi_i,\ \chi_i')$, que j’appellerai, pour abréger, $T_i$, soit cette même substitution suivie d’une substitution du groupe $G'$.

Précisons davantage. Quand on décrit le cycle, le point $x$ décrit dans son plan un contour fermé infiniment petit. En même temps, les points

$$x_0,\quad x_1,\quad x_2,\quad \dots,\quad x_{2p+1},$$

par suite des variations de $y$, décriront des courbes très petites. Deux de ces points, que j’appellerai $x_a$ et $x_b$, sont très voisins l’un de l’autre quand $y$ est voisin de $A_i$. Les autres points $x_k$ décriront des contours fermés quand $y$ tournera autour de $A_i$. Quant à $x_a$ et $x_b$, il pourra arriver qu’ils s’échangent, et alors ils décriront chacun un arc très petit, l’ensemble de ces deux arcs constituant une petite courbe fermée. Ou bien ils ne s’échangeront pas, de sorte que chacun d’eux décrira une courbe fermée.

Si $x$ ne tourne autour d’aucun des points singuliers $x_k$, le point $N$ subira la substitution $T_i$, à laquelle devra par conséquent correspondre, dans le groupe fondamental, la substitution identique.

Si $x$ tourne autour d’un point $x_k$ autre que $x_a$ et $x_b$, $z$ change de signe et le cycle n’est pas fermé ; ce cas doit donc être exclu.

Si $x$ tourne autour des points $x_a$ et $x_b$, la somme des arguments de $x-x_a$ et $x-x_b$ augmente de $2\pi$ ou de $4\pi$. Le premier cas doit être exclu parce que $z$ changerait de signe ; examinons le second.

Reprenons le polygone fuchsien $R$ et les deux polygones partiels $R'$ et $R''$. Au point $x_a$ correspondra sur $R'$ un certain point $u_a$ qui sera le milieu de l’un des côtés (au point de vue non-euclidien). Soit $s_a$ la substitution qui change un point $u$ du plan de $R$ en un point symétrique de $u$ par rapport à $u_a$ (au point de vue non-euclidien).

Soit $u_a'$ un point congruent de $u_a$, transformé de $u_a$ par une substitution $S$ du groupe fuchsien ; et soit $s_a'$ une substitution qui change un point en son symétrique par rapport à $u_a'$. On aura évidemment

$$s_a'=S^{-1} s_a S.$$

Considérons maintenant les différents points du plan de $R$ qui correspondent à $x_b$ ; parmi ces points, je distinguerai celui qui tend vers $u_a$ quand $y$ tend vers $A_i$ sans franchir les coupures $OA$ ; je l’appellerai $u_b$. Je désignerai par $u_b'$ le transformé de $u_b$ par $S$. Je définirai $s_b$ et $s_b'$ par rapport à $u_b$ et $u_b'$ comme $s_a$ et $s_a'$ le sont par rapport à $u_a$ et $u_a'$.

Il est clair que

$$s_a^2=s_b^2={s_a'}^2={s_b'}^2=1,$$

que $s_a s_b$ et $s_b s_a$ appartiennent au groupe fuchsien, que

$$s_b'=S^{-1} s_b S.$$

D’ailleurs, $s_a s_b$ et $s_b s_a$ sont inverses l’une de l’autre.

Cela posé, quand $x$ aura décrit son contour autour de $x_a$ et $x_b$, le point $\xi,\ \eta$ aura subi la substitution $s_a s_b$ (ou la substitution $s_b s_a$, selon le sens dans lequel le contour aura été décrit) ou, plus généralement, une des substitutions du groupe fuchsien.

Le point $N$ aura donc subi la substitution $T_i$ suivie d’une des substitutions $S'$ de $G'$, ou, ce qui revient au même, d’une substitution $S''$ de $G'$ suivie de $T_i$.

A la substitution $T_iS'=T''T_i$ du groupe $G$ correspondra encore dans le groupe fondamental la substitution identique.

Comme nous venons de voir qu’à $T_i$ correspondait déjà la substitution identique, nous devons conclure qu’à $S'$ et $S''$ correspondra également la substitution identique.

Il peut arriver encore que, quand on décrit le cycle fermé sur $V$, $y$ ne tourne pas autours de $A_i$, mais reste très voisin de $A_i$ ; dans ce cas, $\zeta$ et $\zeta'$ reviendront à leurs valeurs primitives ; en même temps, $x$ décrira dans son plan un contour fermé ; on pourra supposer que ce contour entoure les deux points singuliers $x_a$ et $x_b$, puisque, quand $y$ est voisin de $A_i$, ces deux points $x_a$ et $x_b$ sont voisins l’un de l’autre. Alors le point $u$ subit une substitution du groupe fuchsien et le point $N$ subit une substitution $S'''$ de $G'$ à laquelle devra encore correspondre dans le groupe fondamental la substitution identique.

Ainsi, si nous reprenons notre groupe $G$ qui est dérivé du sous-groupe $G'$ et des substitutions $T_i$, nous voyons qu’à toutes les substitutions $T_i$ et à certaines substitutions de $G'$ correspond la substitution identique. Donc le groupe fondamental sera isomorphe à $G'$ (et, par conséquent, au groupe fuchsien), pusqu’à toutes les $T_i$ correspond la substitution identique, et cet isomorphisme sera, en général, mériédrique, parce quà certaines substitutions de $G'$ correspondra, en général, la substitution identique.

Avant d’aller plus loin, une distinction est nécessaire. Il peut arriver que les points singuliers $x_a$ et $x_b$ s’échangent quand $y$ tourne autour de $A_i$, ou bien qu’ils ne s’échangent pas. Dans le premier cas, il n’y a pas de difficulté : la partie de la variété (1) voisine du point $y=A_i$, $x=x_a=x_b$ est assimilable à la partie de la variété

$$z^2=y-x^2$$

voisine de l’origine, et tout cycle fermé qui reste très voisin de ce point est réductible à un point de telle façon que la substitution correspondante du groupe fondamental ne peut être que la substitution identique. Dans ces cas, à $T_i$, à $S'$, à $S''$ correspondra la substitution identique, ainsi que nous venons de l’expliquer.

Dans le second cas, la surface (1) présente un point conique et la portion de la variété (1) voisine de $y=A_i$, $x=x_a=x_b$ est assimilable à la partie de la variété

$$z^2=y^2-x^2$$

voisine de l’origine.

Alors deux conventions également légitimes peuvent être faites : supposons qu’un contour fermé tracé sur $V$ puisse se réduire à un point, mais en franchissant le point conique, et ne le puisse pas autrement. On peut admettre que la substitution correspondante du groupe fondamental est encore la substitution identique, ou, en d’autres termes, on peut traiter le point conique comme un point ordinaire de la variété. Dans ce cas, encore à $T_i$, $S'$ et $S''$ correspondra la substitution identique.

Ou bien on peut faire la convention contraire et traiter le point conique comme un point singulier qu’il est interdit [5] de franchir. Dans ce cas, à $T_i$ correspondra encore la substitution identique, mais il n’en sera plus de même pour $S'''$. On aura d’ailleurs toujours $S''\equiv S'''$.

Voici maintenant la question qui se pose. M. Picard a démontré (cf. Théorie des fonctions algébriques de deux variables, t. I, p. 85 et suiv.) que, si une surface algébrique est la plus générale de son degré, les cycles linéaires peuvent être réduits à des points de telle façon que le nombre de Betti $P_1$ est égal à $1$.

Il ne s’ensuit pas immédiatement que le groupe fondamental se réduise à la substitution identique. En effet, M. Picard a démontré que tout cycle linéaire est homologue à zéro, et, pour démontrer que le groupe fondamental se réduit à la substitution identique, il faudrait faire voir que tout cycle linéaire est équivalent à zéro. Pour la différence entre les homologies et les équivalences, voir Analysis situs, paragraphe 12 (ici).

Il est donc nécessaire de revenir sur la question à ce nouveau point de vue. Voyons d’abord le cas où $p=1$, c’est-à-dire où notre polygone fuchsien $R$ se réduit à un parallélogramme. Alors toutes les substitutions de $G'$ et, par conséquent, toutes celles du groupe fondamental, sont permutables entre elles.

Le groupe $G'$ dérive de deux substitutions que j’appelle $s$ et $s_1$. [6] Soit alors un cycle quelconque ; à ce cycle correspondra une substitution de $G'$ qui pourra s’écrire, par exemple,

$$s^\alpha s_1^{\alpha_1} s_\beta s_1^{\beta_1} s^\gamma s_1^{\gamma_1}.$$

Les substitutions de $G'$ étant permutables, elle pourra s’écrire également

$$s^{\alpha + \beta + \gamma} s_1^{\alpha_1 + \beta_1 + \gamma_1}.$$

Si, comme l’a démontré M. Picard, tout cycle est homologue à zéro, cela veut dire que, parmi les cycles possibles, il y en a deux correspondant aux substitutions de $G'$

$$s^a s_1^b,\qquad s^c s_1^d$$

(où $a$, $b$, $c$, $d$ sont quatre entiers dont le déterminant n’est pas nul) et qui sont susceptibles de se réduire à un point. Il arriverait alors qu’à $s^a s_1^b$ et à $s^c s_1^d$ correspondra dans le groupe fondamental la substitution identique, ce que j’écrirai

$$s^a s_1^b \equiv 1,\qquad s^c s_1^d \equiv 1.$$

Nous en conclurons, en nous rappelant que $s$ et $s_1$ sont permutables,

$$s^\epsilon \equiv 1,\qquad s_1^\epsilon \equiv 1,\qquad \epsilon=ad - bc.$$

On voit que le groupe fondamental ne pourrait, en tout cas, compredre qu’un nombre fini de substitutions, au plus $\epsilon^2$.

Mais on peut aller plus loin, même dans le cas de $p>1$.

Supposons, pour fixer les idées, que $p=2$ et appelons, pour abréger

$$a,\quad b,\quad c,\quad d,\quad e,\quad f$$

les six points singuliers du plan des $x$ que nous appelions jusqu’ici $x_0,\dots,x_6$. [7]

Soit d’abord $y=0$ ; joignons le point $x=0$ aux points $a$, $b$, $c$, $d$, $d$, $f$ par des coupures rectilignes, de telle façon qu’en tournant autour du point $O$ on rencontre ces coupures dans l’ordre [8]

$$Oa,\quad Ob,\quad Oc,\quad Od,\quad Oe,\quad Of.$$

Faisons maintenant varier $y$ d’une manière continue, mais sans franchir aucune des coupures $OA_i$ ; en même temps les points $a,b,\,\dots$, se déplaceront d’une manière continue, mais sans s’échanger ou sans tourner les uns autour des autres ; les coupures $Oa,\ \dots$, se déplaceront et même cesseront d’être rectilignes, mais on les rencontrera toujours dans le même ordre en tournant autour de $O$.

Quand on franchira la coupure $Oa$, la variable $u$ (argument des fonctions fuchsiennes) subira une transformation que j’appellerai $a$ et qui sera une sorte de symétrie analogue à la substitution $s_a$ définie plus haut (symétrie par rapport à $u_a$).

Je définirai, de même, les transformations $b$, $c$, $d$, $e$, $f$ ; il est clair qu’on aura

$a^2=b^2=c^2=d^2=e^2=f^2$	$=1$,
$abcdef$	$=1$,

et que ce sont là les seules relations qu’il y ait entre elles. Le groupe fuchsien sera formé de toutes les combinaisons possibles de ces transformations prises en nombre pair.

Lorsque $y$ tend vers $A_i$, deux des points singuliers, $a$ et $d$, par exemple, se rapprochent l’un de l’autre ; quand $y$ tourne autour de $A_i$, ces deux points s’échangeront (dans le cas général où le point $x=a$, $y=A_i$ n’est pas un point double de la surface, cas général que nous examinerons d’abord).

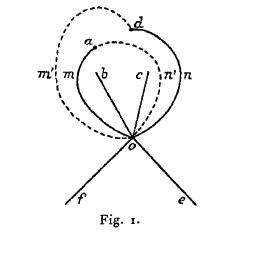
Quand le point $y$ est voisin de $A_i$ (mais sans avoir franchi la coupure $OA_i$), les quatre coupures $Oa$, $Ob$, $Oc$, $Od$ présentent la disposition représentée en trait plein sur la figure 1 ; après que le point $y$ a décrit un contour autour de $OA_i$, les coupures $Oa$ et $Od$ se sont déformées et ont pris la forme représentée en trait pointillé sur la figure. Elles se sont d’ailleurs permutées de telle façon que la coupure en trait plain $Oma$ est devenue la coupure en trait pointillé $Om'd$, tandis que la coupure $Ond$ est devenue $On'd$.

Traçons maintenant dans le plan un contour fermé quelconque, partant d’un point fixe $M_0$ quelconque du plan ; si ce contour coupe successivement les coupures $Oa$, $Oc$, $Oa$, $Ob$, $Of$, $Oe$, par exemple, il équivaudra à la substitution $acabfe$.

Cela posé, considérons un contour fermé coupant l’une des coupures

$$\tag{1} Oma,\quad Ob,\quad Oc,\quad Ond,\quad Oe,\quad Of, $$

et une seule ; quand $y$ aura tourné autour de $A_i$, il se transformera en un contour coupant une des coupures

$$\tag{2} Om'd,\quad Ob,\quad Oc,\quad On'a,\quad Oe,\quad Of, $$

et une seule.

Or, il est aisé de voir sur la figure qu’un contour coupant l’une des coupures (2) coupera dans un certain ordre certaines des coupures (1b) et équivaudra, par conséquent, à une certaine combinaison des substitutions $a$, $b$ et $c$.

Si nous supposons, par exemple, $M_0$ extérieur au contour $Om'dna$. [9] Le cycle qui coupe :

$Om'd$	coupera	$Ond$	et équivaudra à	$d$
$Ob$	>>	$Ond$, $Oma$, $Ob$, $Oma$ et $Ond$	>>	$dabad$,
$Oc$	>>	$Ond$, $Oma$, $Oc$, $Oma$ et $Ond$	>>	$dacad$,
$Om'a$	>>	$Ond$, $Oma$ et $Ond$	>>	$dad$,
$Oe$	>>	$Oe$	>>	$e$,
$Of$	>>	$Of$	>>	$f$.

Par conséquent, la transformation $T_i$ changera les substitutions

$$\tag{3} a,\quad b,\quad c,\quad d,\quad e,\quad f $$

respectivement en

$$\tag{4} d,\quad dabad,\quad dacad,\quad dad,\quad e,\quad f. $$

Nous avons, plus haut, écrit la relation

$$T_iS'=S''T_i,$$

et montré qu’aux deux substitutions $S'$ et $S''$ de $G'$ doit correspondre la même substitution du groupe fondamental, ce que nous écrirons :

$$\tag{5} S'\equiv S''. $$

Comme $S'$ est une certaine combinaison des substitutions (3) en nombre pair et que $S''$ est la combinaison correspondante des substitutions (4), il suffit, pour que l’équivalence (5) ait lieu, que l’on ait

$$a \equiv d,\qquad b \equiv dabad,\qquad c \equiv dacad,\qquad d \equiv dad.$$

Or, toutes ces équivalences se réduisent à

$$ad\equiv 1$$

ou, ce qui revient au même, à $a\equiv d$.

Nous avons vu ensuite qu’à la substitution $S'''$ de $G'$ doit correspondre la substitution identique du groupe fondamental, ce que j’écris

$$S'''\equiv 1.$$

On voit ici que $S'''$ n’est autre chose que $ad$, de sorte que nous retombons toujours sur la même équivalence

$$ad \equiv 1$$

qui est (avec $T_i \equiv 1$) la seule que l’on puisse déduire de la considération du point singulier $A_i$.

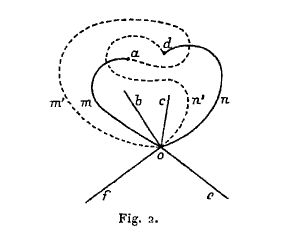
Il nous reste à examiner le cas où le point

$$x=a,\qquad y=A_i$$

est un point conique de la surface $z=F(x,y)$. Refaisons une figure analogue à la figure 1. Quand le point $y$ tournera autour de $A_i$, les coupures en trait plein $Oma$ et $Ond$ se changeront dans les coupures $Om'a$ et $On'd$ en trait pointillé (fig. 2). En raisonnant comme tout à l’heure et considérant les différents cycles qui partent du point $M_0$ et qui coupent une des coupures, et une seule, on voit que le cycle qui coupe

$Om'a$	coupera	$Ond$, $Oma$ et $Ond$,
$Ob$	>>	$Ond$, $Oma$, $Ond$, $Oma$, $Ob$, $Oma$, $Ond$, $Oma$, $Ond$,
$Oc$	>>	$Ond$, $Oma$, $Ond$, $Oma$, $Oc$, $Oma$, $Ond$, $Oma$, $Ond$,
$On'd$	>>	$Ond$, $Oma$, $Ond$, $Oma$, $Ond$,
$Oe$	>>	$Oe$
$Of$	>>	$Of$.

Ces cycles équivaudront donc respectivement aux combinaisons

$$dad,\quad dadabadad, \quad dadacadad, \quad dadad,\quad e,\ f,$$

c’est-à-dire que $T_i$ transformera les substitutions

$$a,\quad b,\quad c,\quad d,\quad e,\quad f$$

dans les substitutions

$$dad,\quad dadabadad, \quad dadacadad, \quad, dadad,\quad e,\quad f.$$

Si l’on traite le point conique comme un point ordinaire de la variété, on aura encore

$$S' \equiv S'',\quad S'''\equiv 1.$$

La première condition entraîne

$$\tag{6} a \equiv dad,\quad b \equiv dadabadad,\quad c \equiv dadacadad, \quad d \equiv dadad. $$

La seconde nous donne simplement

$$ad \equiv 1,$$

ce qui entraîne d’ailleurs les conditions (6).

Considérons maintenant le point conique comme un point qu’il est interdit de franchir. Alors nous aurons encore $S' \equiv S''$ et, par conséquent, les conditions (6) mais nous n’aurons plus $S''' \equiv 1$, c’est-à-dire $ad \equiv 1$.

Les conditions (6) se ramènent à une seule

$$(ad)^2 \equiv 1.$$

Ainsi, si nous nous interdisons de franchir le point conique, nous n’aurons pas $ad \equiv 1$, mais nous aurons $(ad)^2 \equiv 1$.

Ainsi, le cycle qui tourne autour de deux points $a$ et $d$ n’est pas la frontière d’une variété à deux dimensions faisant partie de $V$, tandis que ce cycle pris deux fois constitue la frontière d’une variété à deux dimensions faisant partie de $V$, si du moins l’on suppose que toutes ces variétés à une ou à deux dimensions ne s’écartent pas beaucoup du point conique.

Il est aisé de rapprocher ceci d’un fait connu. Nous avons déjà fait remarquer que la portion de $V$ voisine du point conique est homéomorphe à la portion de la variété $z^2 = x^2-y^2$ ou de la variété $z^2 = xy$ voisine de l’origine.

Appelons donc $W$ la variété à quatre dimensions $z^2 = xy$, dont on suppose que l’on a exclu l’origine qui est un point conique. Ce qui précède nous enseigne qu’il y a sur $W$ un cycle fermé $C$ à une dimension tel que l’on n’ait pas l’équivalence

$$C \equiv 0,$$

mais que l’on ait l’équivalence

$$2C \equiv 0.$$

Or, considérons la variété à trois dimensions

$$z^2 = xy,\qquad |x^2| + |y^2| = 1$$

que j’appelle $W'$. C’est la variété envisagée par M. Heegaard [cf. Premier Supplément à l’Analysis situs (Rendiconti del Circolo matematico di Palermo, t XIII, 1899)].

A tout point, $x,y,z$ de $W$ correspond un point

$$\frac{x}{\sqrt{|x^2| + |y^2|}},\quad \frac{y}{\sqrt{|x^2| + |y^2|}},\quad \frac{z}{\sqrt{|x^2| + |y^2|}}.$$

Si le point de $W$ décrit un cycle $C$, le point correspondant de $W'$ décrira un cycle $C'$. Or, il est évident que si sur $W$ on a $C \equiv 0$, sur $W'$ on aura $C' \equiv 0$, et réciproquement. (Je rappelle que l’équivalence $C \equiv 0$ signifie qu’il existe sur $W$ une variété à deux dimensions dont $C$ est la frontière complète).

Si donc sur $W$ on a $2C \equiv 0$ sans avoir $C \equiv 0$, il y aura sur $W'$ un cycle $C$ tel que $2C' \equiv 0$ sans que $C' \equiv 0$.

Or, on se rappelle que l’existence d’un pareil cycle $C'$ est une des propriétés caractéristique de la variété de M. Heegaard.

Rien n’est plus facile maintenant que de déterminer le groupe fondamental. Ce groupe est mériédriquement isomorphe au groupe fuchsien, lequel dérive de toutes les combinaisons en nombre pair des substitutions $a$, $b$, $c$, $d$, $e$, $f$, lesquelles sont supposées liées par les relations

$$a^2 = b^2 = c^2 = d^2 = e^2 = f^2 = 1, \qquad abcdef = 1.$$

Mais si les deux points $a$ et $d$ peuvent s’échanger quand $y$ tourne autour de $A_i$, on aura $ad \equiv 1$, d’où

$$a \equiv d.$$

Je dis que la même relation subsistera si $a$ se change en $d$ quand $y$ décrit un cycle fermé quelconque, enveloppant, par exemple, non plus un seul point singulier, mais deux points singuliers $A_i$ et $A_k$. Si, en effet, par exemple, $a$ s’échange avec $b$ quand $y$ tourne autour de $A_i$ et $b$ avec $d$ quand $y$ tourne autour de $A_k$ (de telle façon que $a$ se change en $d$ quand $y$ décrit le contour qui enveloppe à la fois ces deux points singuliers), on aura

$$a \equiv b, \qquad b \equiv d$$

et, par suite,

$$a \equiv d.$$

C. Q. F. D.

Si donc les points singuliers $a$, $b$, $c$, $d$ sont susceptibles de s’échanger entre eux, on aura

$$a \equiv b \equiv c \equiv d.$$

Si le polynome $F(x,y)$ est indécomposable, les racines de l’équation

$$F(x,y) = 0$$

(considérée comme équation en $x$) seront toutes susceptibles de s’échanger entre elles quand on fera varier $y$ d’une façon quelconque.

Nos $2p+2$ points singuliers (qui sont au nombre de six, $a$, $b$, $c$, $d$, $e$, $f$ si $p=2$) s’échangeront donc tous les uns avec les autres et l’on aura

$$a \equiv b \equiv c \equiv d \equiv e \equiv f.$$

Une substitution quelconque du groupe fondamental, se réduisant à une combinaison en nombre pair de $a$, $b$, $c$, $d$, $e$, $f$, se réduira à une puissance paire de $a$, c’est-à-dire à la substitution identique.

Ainsi, si le polynome $F$ est indécomposable, le groupe fondamental se réduit à une seule substitution qui est la substitution identique.

Si le polynome $F$ se décompose en deux facteurs $F = F_1F_2$, nous devrons distinguer deux sortes de points singuliers : ceux qui satisfont à l’équation $F_1 = 0$ et ceux qui satisfont à $F_2 = 0$ ; supposons, par exemple, que $a$, $b$, $c$, $d$ satisfassent à $F_1 = 0$, $e$ et $f$ à $F_2 = 0$ ; on aura alors

$$a \equiv b \equiv c \equiv d, \qquad e \equiv f.$$

On n’aura pas $a \equiv e$ (si les points coniques ne sont pas regardés comme des points ordinairs) ; mais on aura $(ae)^2 \equiv 1$, de sorte que le groupe fondamental comprendra seulement deux substitutions

$$1,\quad ae.$$

Il faut voir encore si ce nombre n’est pas réduit par la considération de la relation

$$\tag{7} abcdef = 1. $$

Observons que l’on doit toujours réduire le degré de $F$ à être pair (au besoin par une transformation homographique), puisque le nombre des points singuliers est $2p+2$. Nous devons alors distinguer le cas où $F_1$ et $F_2$ sont tous deux de degré pair : alors la relation (7) se réduit à une identité et le groupe fondamental n’est pas réduit ; et le cas où $F_1$ et $F_2$ sont tous deux de degré impair : alors la relation (7) se réduit à $ae \equiv 1$ et le groupe fondamental ne comprend plus qu’une substitution.

Si $F$ se décompose en trois facteurs $F = F_1F_2F_3$, que $a$ soit l’une des racines de $F_1 = 0$, $b$ l’une de celles de $F_2 = 0$, $c$ l’une de celles de $F_3 = 0$, on aura

$$ a^2 \equiv b^2 \equiv c^2 \equiv 1,\qquad (ab)^2 \equiv (bc)^2 \equiv (ac)^2 \equiv 1,$$

ce qui montre que le groupe fondamental se réduit à quatre substitutions

$$1, \quad ab, \quad bc, \quad ac,$$

ce nombre pouvant encore être réduit, à cause de la relation (7), si deux des facteurs sont de degré impair.

Si, enfin, $F$ se décompose en $n$ facteurs $F = F_1F_2\dots F_n$ ; si $a_i$ est l’une des racines de $F_i=0$ ; on aura

$$\tag{8} a_i ^2 \equiv 1,\qquad (a_ia_k)^2 \equiv 1\qquad (i,k = 1,\,2,\,\dots,\, n). $$

Soit alors $S$ une substitution quelconque du groupe fondamental ; ce sera le produit d’un nombre pair de substitutions $a_i$. Mais des relations (8) on peut déduire

$$a_ia_k \equiv a_ka_i.$$

On peut donc permuter les facteurs de $S$ et l’écrire sous la forme

$$a_1^{\epsilon_1}a_2^{\epsilon_2}\dots a_n^{\epsilon_n} \quad (\epsilon_1 + \epsilon_2 + \dots + \epsilon_n \equiv 0,\ \mathrm{mod}\ 2).$$

On peut ensuite, à l’aide des relations (8), réduire les exposants $\epsilon$ à $0$ ou à $1$, de sorte que $S$ se réduira à un produit de $k$ facteurs $a_1,\,a_2,\,\dots,\,a_n$, les $k$ facteurs étant differents et $k$ étant pair, l’ordre des facteurs étant d’ailleurs regardé comme indifférent. Il y a $2^{n-1}$ combinaisons possibles ; le groupe fondamental comprend donc $2^{n-1}$ substitutions ; mais ce nombre peut être réduit de moitié par le moyen de la relation (7), si deux ou plusieurs facteurs sont de degré impair.