Entre la définition formelle d’un concept mathématique et la manière dont un mathématicien le comprend, il y a souvent un immense fossé. Le rôle d’un cours de mathématiques, écrit ou oral, est bien entendu de donner la définition formelle des objets : « Une variété est un espace topologique tel que tout point possède un voisinage bla-bla-bla », mais il faut aussi essayer de transmettre des intuitions. C’est en tous les cas ce que ce site essaye de faire.

Dans cette interview de Egbert Brieskorn, Henri Paul recommande au débutant d’écouter le chapitre « Shared understandings, manifolds, and definitions ». On y apprend, sur l’exemple des variétés, comment chacun se forge son intuition, qui n’est pas nécessairement la même que celle du collègue, mais que ce n’est pas très grave. Très intéressant…

« What do I have in mind when I say « manifold » ? »

Brieskorn rappelle l’un des premiers exemples de variétés, donné par Riemann dans son article fondateur : l’« espace des couleurs ». Cet espace n’est en aucun cas une sous-variété d’un espace euclidien et on peut l’aborder de nombreuses manières différentes.

La position des objets sensibles et les couleurs sont probablement parmi les notions les plus simples qui permettent de définir des variétés de dimensions variées.

Riemann, 1854.

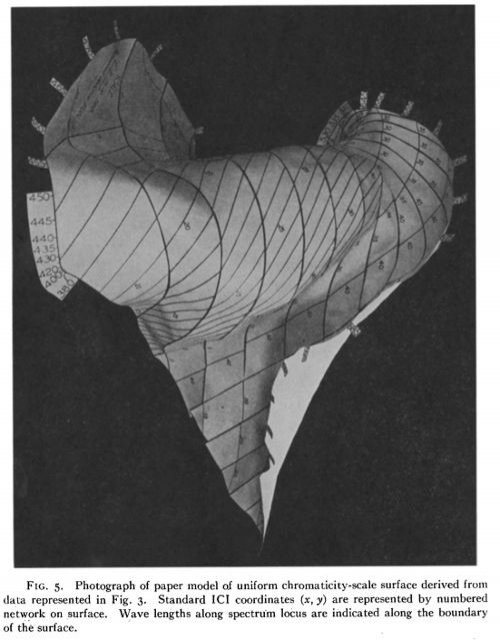
Pour l’amusette, David L. Macadam (du laboratoire de recherche de Kodak) a tenté en 1944 de représenter la géométrie de l’espace des couleurs en collant des bouts de papier. Voici le modèle obtenu. Son article « The geometry of color space » est très intéressant. Plus récemment, certains auteurs ont même calculé la courbure de l’espace des couleurs.

Mais pour convaincre le lecteur que des mathématiciens différents peuvent avoir des idées différentes sur les variétés, Henri Paul recommande de visionner cette conférence de M. Gromov : What is a manifold ?.