
Ah ! La fibration de Hopf. Quelle merveille ! Tout étudiant en topologie algébrique doit l’étudier, en détail. Ça ne se discute pas, voilà tout. C’est un ordre de Henri Paul.
Le lecteur pourra observer la fibration de Hopf dans les chapitres 7 et 8 de Dimensions.
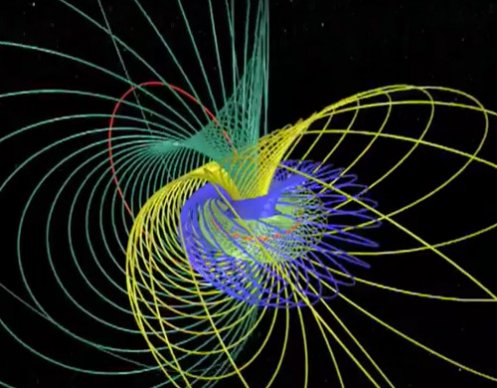
Voici deux « exercices » sur la fibration de Hopf :
- Bien sûr, comme d’habitude, ce n’est pas Hopf qui l’a inventée. La contribution de Hopf (attention à ne pas confondre : il s’agit de Heinz Hopf (1894-1971) et non pas de Eberhard Hopf (1902-1983) ; Eberhard est un cas unique d’un mathématicien allemand, en poste aux USA qui a décidé de rentrer en Allemagne en 1936, dans le sens opposé du flux de mathématiciens à cette époque) est différente. Il a montré que « sa » fibration ${\mathbb S}^3 \to {\mathbb S}^2$ n’est pas homotope à une application constante, alors que toutes les applications induites en homologie sont triviales. Cet article raconte l’histoire. Essayez de démontrer ce théorème de Hopf. Le fait que deux fibres soient enlacées est important.
- La sphère ${\mathbb S}^3$ de dimension 3 est un groupe : le groupe des quaternions unitaires. Chaque plongement du corps des complexes dans le corps des quaternions fournit un plongement de $SO(2)$ dans ${\mathbb S}^3$ qui à son tour définit une « fibration de Hopf » : ${\mathbb S}^3 \to {\mathbb S}^3/SO(2)$. Ainsi « la » fibration de Hopf n’est pas unique puisque l’espace des plongements de $\mathbb C$ dans les quaternions est une sphère de dimension 2 (vérifiez-le). Essayez d’imaginer toutes ces fibrations simultanément. D’autre part, au lieu de considérer les classes à droite ${\mathbb S}^3/SO(2)$, on peut considérer les classes à gauche $SO(2)\backslash {\mathbb S}^3$, ce qui fait encore d’autres fibrations.


