Quand on éclate un point du plan, on obtient une bande de Mœbius. Dit autrement, si on implose le cercle qui est le cœur de la bande de Mœbius, on obtient un plan.

Voici une œuvre, dûe à Sylvie Pic, dans laquelle on voit ce qui se passe quand on collapse le cœur d’une bande de Moebius.

Clairement, l’objet final est un cône sur un cercle tracé sur la sphère : c’est donc un disque (topologiquement), comme il se doit. Quelle est cette courbe sur la sphère ? IL s’agit du folium de Descartes, dont l’équation est

$$ x^3+y^3= xy. $$

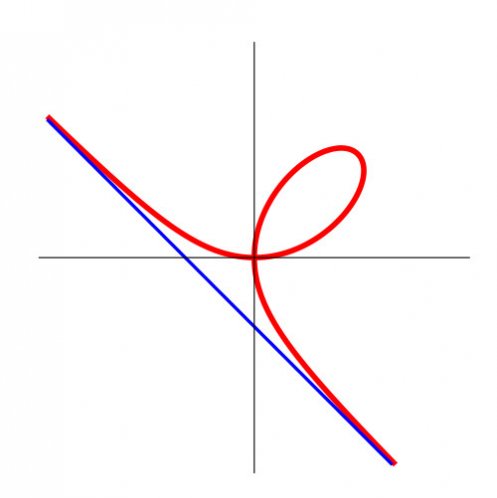
Dit autrement, le cône sur cette courbe est la surface cubique singulière d’équation

$$ x^3+y^3= xyz. $$

On trouve un modèle de cette surface parmi les objets mathématiques de Goettingen.

Pouvez-vous justifier tout cela ?

Pour en savoir plus, et regarder de jolies figures, vous pouvez lire le chapitre Mœbius and his band de A Singular Mathematical Promenade.