

Les « cycles évanescents » dont il est question sont-ils dus à Picard ou Lefschetz ? Aucun des deux ! Le processus a été long et on peut penser que la terminologie est due à Euler !
Dans son « textbook » célèbre datant de 1748 intitulé « Introductio in analysin infinitorum », volume 2, Euler étudie comment varie la topologie (sans utiliser ce mot bien sûr) d’une courbe algébrique lorsque ses coefficients dépendent d’un paramètre. Il suit l’exemple de Newton en se concentrant sur les courbes du troisième degré, de la forme :
$$ xy^2= 2by+ax^2+cx+d-n^2x^3. $$
Tout dépend du nombre de racines réelles de $F=b^2+dx+cx^2+ax^3-n^2x^4$. Euler trace les courbes dans chaque cas, mais surtout il cherche à décrire ce que nous appellerions aujourd’hui les « bifurcations ». Dans l’extrait suivant, on lit « tum nodus in cuspidem acutissimam evanescet, … ».
Evanescet… Un ovale évanescent.

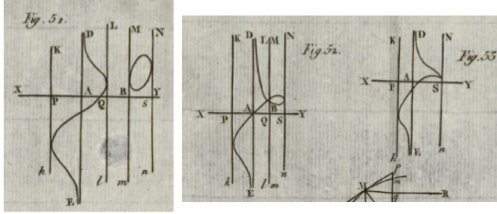
A vos Gaffiot !